FM調頻 - moerjielovecookie

1 調制アルゴリズム#

1.1 FM 信号の説明#

基底帯域調制信号を使用してキャリア信号の瞬時周波数を制御し、調制信号の規則に従って変化させる。このプロセスは、調制信号がアナログ信号であるとき、周波数変調（FM）と呼ばれる。FM 信号の時域表現は次のようになる：

S_{FM}(t)=A_m\times \cos[\omega_ct+K_f \int^{t}_{0}m(\tau)d\tau]\tag{1}

ここで、$A_m$ はキャリア振幅、$K_f$ は周波数変調感度（単位は $rad/(s\cdot V)$）、$m (t)$ は調制信号、$cos\omega_c t$ はキャリア、$\omega_c$ はキャリア角周波数。
式 (1) に基づいて、FM 信号のキャリア周波数に対する瞬時周波数偏差は次のように計算できる：

\frac{d\left[K_f\int_0^tm(\tau)d\tau\right]}{dt}=K_fm(t)\tag{2}

式（1）から、FM 信号のキャリア位相に対する瞬時位相偏移は $m (t)$ の積分に対して線形に変化し、式（2）から、FM 信号のキャリア周波数に対する瞬時周波数の変化は $m (t)$ に対して線形に変化し、比例係数はすべて $K_f$ である。$k_f$ を周波数変調感度（単位 Hz/V）で表すと、関係は $K_f=2\pi k_f$ となる。
FM の周波数変調指数 $\beta$ は次のようになる：

\beta=\frac{k_f |m(t)|_{max}}{W}\tag{3}

ここで $W$ は基底帯域信号 $m (t)$ の帯域幅または最高周波数。

1.1.1 ナローバンド周波数変調（NBFM）#

$m (t)$ によって引き起こされる最大瞬時位相偏移が 30° 未満の状況をナローバンド周波数変調と呼ぶ。ナローバンド周波数変調の帯域幅は狭く、データ伝送量は限られており、主に無線音声の伝送に使用される。

|K_f\int_0^tm(\tau)d\tau|\ll\frac\pi6 \tag{4}

このとき、式（1）は次のように近似できる：

\begin{aligned}s_{NBFM}(t)&=Acos\left[\omega_ct+K_f\int_0^tm(\tau)d\tau\right]\\\\&=Acos(\omega_ct)cos{\left[K_f\int_0^tm(\tau)d\tau\right]}-Asin(\omega_ct)sin{\left[K_f\int_0^tm(\tau)d\tau\right]}\\\\&\approx Acos(\omega_ct)\cdot1-Asin(\omega_ct)\cdot K_f\int_0^tm(\tau)d\tau\\\\&=Acos(\omega_ct)-\left[AK_f\int_0^tm(\tau)d\tau\right]sin(\omega_ct)\end{aligned}\tag{5}

これを FFT 変換すると、ナローバンド周波数変調信号の周波数スペクトルは次のようになる：

S_{NBFM}(\omega)=\pi A\left[\delta(\omega+\omega_c)+\delta(\omega-\omega_c)\right]+\frac{AK_f}{2}\left[\frac{M(\omega-\omega_c)}{\omega-\omega_c}-\frac{M(\omega+\omega_c)}{\omega+\omega_c}\right]\tag{6}

ここで $M (\omega)$ は調制信号 $m (t)$ の周波数スペクトルである。AM 信号とは異なり、NBFM 信号の 2 つのサイドバンドはそれぞれ因子 $1/(\omega-\omega_c)\text { と } 1/(\omega+\omega_c)$ を掛けられており、因子は周波数に依存する関数であるため、その加重は周波数加重であり、加重の結果は調制信号の周波数スペクトルの歪みを引き起こし、さらに NBFM の一つのサイドバンドは AM と逆相である。

1.1.2 ワイドバンド周波数変調（WBFM）#

式（4）の条件を満たさない場合は、ワイドバンド周波数変調と呼ばれる。ワイドバンド周波数変調は広い周波数帯域を占有し、大量のデータを伝送するため、主に FM ステレオ放送に使用される。WBFM の時域表現は簡略化できず、$m (t)=A_m \cos (\omega_m t)$ のとき、式（1）に代入すると次のようになる：

\begin{aligned}s_{WBFM}(t)&=Acos\left[\omega_ct+K_f\int_0^tA_mcos(\omega_m\tau)d\tau\right]\\\\& =Acos\left[\omega_ct+\frac{K_fA_m}{\omega_m}sin(\omega_mt)\right]\\\\& =Acos[\omega_ct+\beta sin(\omega_mt)]\\\\& =A\sum_{n=-\infty}^\infty J_n(\beta)cos[(\omega_c+n\omega_m)t]\end{aligned}\tag{7}

式中の $J_n (\beta)$ は第一種 n 次ベッセル関数であり、周波数変調指数 $\beta$ の関数である。
周波数スペクトルは次のようになる：

S_{WBFM}(\omega)=\pi A\sum_{n=-\infty}^\infty J_n(\beta)\left[\delta(\omega-\omega_c-n\omega_m)+\delta(\omega+\omega_c+n\omega_m)\right]\tag{8}

1.2 FM 信号の帯域幅#

ワイドバンド周波数変調信号の周波数スペクトルは無限の周波数成分を含むため、理論的には周波数変調信号の帯域幅は無限大である。しかし、実際にはサイド周波数の振幅 $J_n (\beta)$ は n の増加に伴い減少するため、適切な n 値を選択してサイド周波数成分が無視できる程度まで小さくすることで、FM 信号は有限の帯域幅を持つと近似できる。通常の原則は信号の帯域幅は、未調整キャリアの 10% 以上の振幅を持つサイド周波数成分を含むべきである。経験則によれば、$\beta \geq 1$ のとき、サイド周波数数 $n=\beta +1$ を選択すればよい。なぜなら、$\beta+1$ より大きいサイド周波数の振幅はすべて 0.1 未満であるからである。
この経験則に基づいて、FM 信号の有効帯域幅は次のようになる：

BW_{FM}=2(\beta+1)W\tag{9}

この公式はカーソンの公式である。

2 FM 調制方法#

2.1 直接調頻法#

直接調頻法は、調制信号 $m (t)$ を使用して高周波発振器を直接制御し、ループ素子のパラメータを変更して、出力周波数が調制信号の規則に従って線形に変化するようにする。一般的に使用される素子は可変容量ダイオードである。直接調頻法の主な利点は、線形調頻の要件を満たしながら大きな周波数偏差を得ることができ、回路が簡単であることである。主な欠点は、周波数の安定度が高くないことであり、しばしば自動周波数制御システムを使用して中心周波数を安定させる必要がある。

2.2 間接調頻法#

間接調頻法は倍周法とも呼ばれる。まず調制信号を積分し、次にキャリアの位相を調整して NBFM 信号を生成し、$n$ 回の倍周器を経て WBFM 信号を得る。利点は周波数の安定性が高いことであり、欠点は何度も倍周と混合を行う必要があり、回路が複雑であることである。

2.3 正交調制法#

式（1）を三角展開すると、次のようになる：

\begin{aligned}s_{FM}(t)&=Acos\left[\omega_ct+K_f\int_0^tm(\tau)d\tau\right]\\\\&=Acos(\omega_ct)cos\left[K_f\int_0^tm(\tau)d\tau\right]-Asin(\omega_ct)sin{\left[K_f\int_0^tm(\tau)d\tau\right]}\end{aligned}\tag{10}

プロセスは次のようになる：

調制信号 $m (t)$ を積分し、$\Phi=K_f\int^{t}_{0} m (\tau) d\tau$ を得る
積分後の信号からコサインとサインをそれぞれ取り、I 路データ $I (t)=\cos (\Phi)$ と Q 路データ $Q (t)=\sin (\Phi)$ を得る
それぞれキャリア $A\cos (\omega_c t)$ と $-A\sin (\omega_ct)$ を掛けて加算すると、FM 信号 $s_{FM}(t)=I (t) Acos (\omega_ct)-Q (t) Asin (\omega_ct)$ が得られる

3 FM 信号フォーマット#

我が国の FM システムの調制周波数偏差は 150kHz で、87MHz〜107.9MHz の周波数帯域に分布している。
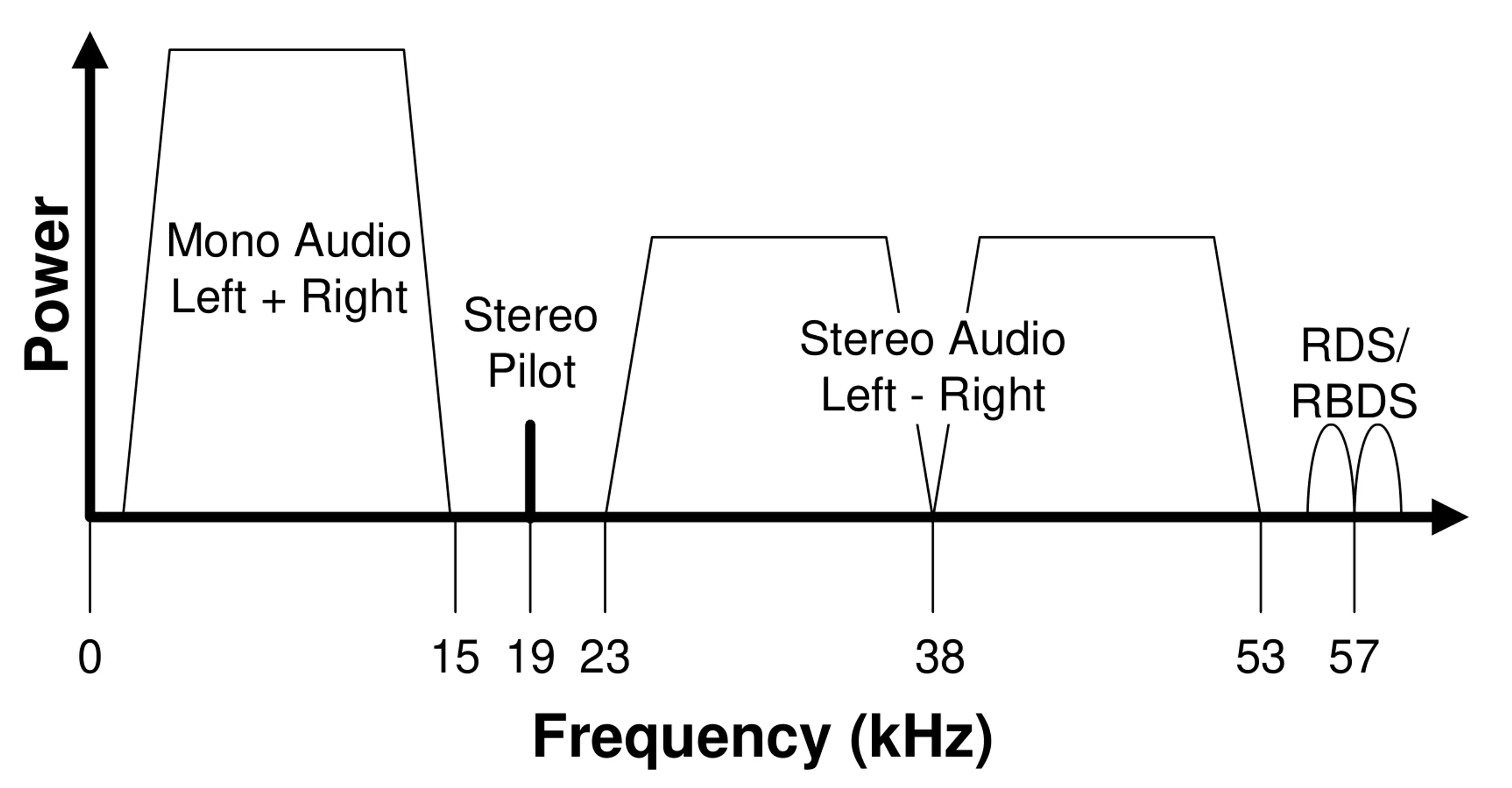
基底帯域信号は MPX 信号であり、モノラル（0〜15kHz）、導波（19kHz）、ステレオ副搬送波（中心周波数 38kHz）、RDS データ（中心周波数 58kHz）を含む。その周波数スペクトル成分は次の通りである：
MPX 信号の周波数成分