moerjielovecookie

Sawen_Blog

一个普通工科牲的博客网站
x
github
follow
email
ホームアーカイブFPGA数字通信友链

多速率信号処理-CICフィルター

#数字通信22
AI 翻訳
この記事はAIを通じて英語から日本語に翻訳されました。原文を表示
AI が生成した要約
# 多速率信号处理-CIC滤波器 级联积分梳状滤波器（CIC滤波器）是一种高效的数字滤波器，具有低通滤波器的特性，且设计时不需要存储滤波器系数，节省存储空间。其结构规则，能够灵活设置插值因子。 ## 积分器 积分器的时域表示为 \( y_1(n) = x(n) + y_1(n-1) \)，频域表示为 \( H_1(e^{jw}) = \frac{1}{1 - e^{-jw}} \)。积分器只有极点，对直流信号增益无限大。 ## 梳状滤波器 梳状滤波器的时域表示为 \( y_C(n) = x(n) - x(n-RM) \)，频域表示为 \( H_C(z) = 1 - z^{-RM} \)。它只有零点。 ## 单级CIC滤波器 单级CIC滤波器的幅度谱为 \( |H_{CIC}(e^{j\omega})| = \left|\frac{\sin\left(\frac{RM}{2}w\right)}{\sin\left(\frac{w}{2}\right)}\right| \)。其主瓣区间为 \( [0, \frac{2\pi}{RM}] \)，旁瓣电平和阻带衰减可通过多级CIC级联改善。 ## 位宽问题 多级CIC滤波器的最大增益为 \( G_{max} = (RM)^N \)。输出的最大位宽为 \( B_{out} = \text{ceil}[\log_2|y_{max}|] + 1 = N \cdot \text{ceil}[\log

1 基本原理#

級聯積分コームフィルター（Cascade Integrator Comb）は、多速率信号処理において非常に効率的なデジタルフィルターです。CIC フィルターはローパスフィルターの特性を持ちながら、以下の利点があります：

  • フィルター係数がすべて 1 であり、設計時にフィルター係数を保存する必要がなく、ストレージユニットを節約し、フィルタリング時には加算器と累積器のみが必要で、乗算器は不要です。
  • 構造が規則的であり、全体の構造に影響を与えずに補間因子を柔軟に設定できます。

1.1 積分器#

積分器の構造は

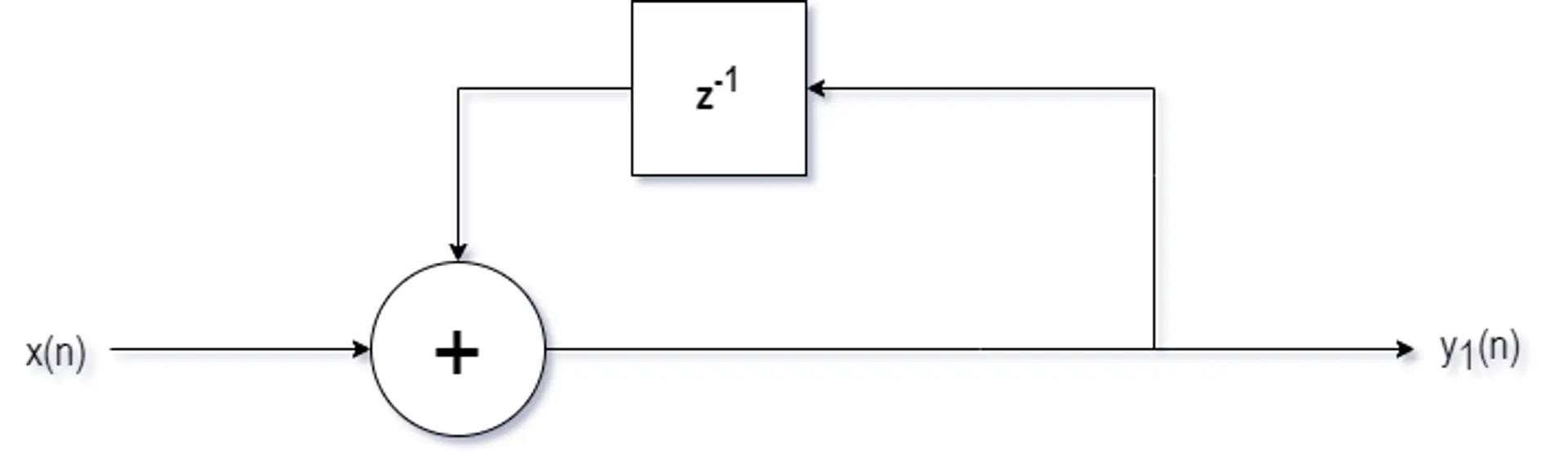
2024after4202409052106726.png

時域では次のように表されます

y1(n)=x(n)+y1(n−1)y_1(n)=x(n)+y_1(n-1)

周波数域では次のように表されます

H1(ejw)=11−e−jwH_1(\mathrm{e}^{\mathrm{j}w})=\frac{1}{1-\mathrm{e}^{-\mathrm{j}w}}

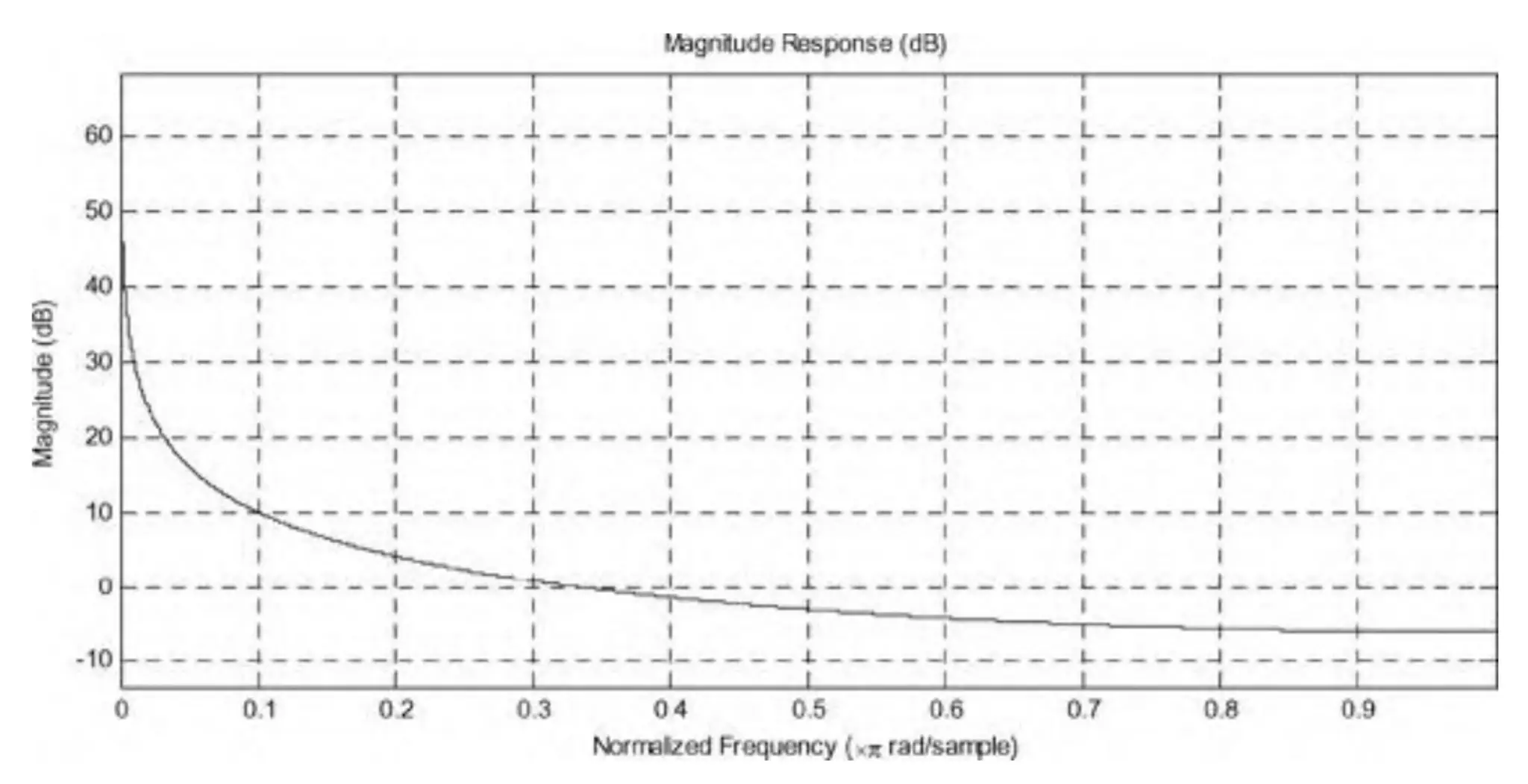
積分器の振幅スペクトルは次のようになります

∣H1(ejw)∣=∣11−e−jw∣=∣1e−jw/2(ejw/2−e−jw/2)∣=∣12sin⁡(w2)∣\left|H_1(\mathrm{e}^{jw})\right|=\left|\frac{1}{1-\mathrm{e}^{-jw}}\right|=\left|\frac{1}{\mathrm{e}^{-jw/2}(\mathrm{e}^{jw/2}-\mathrm{e}^{-jw/2})}\right|=\left|\frac{1}{2\sin\left(\frac{w}{2}\right)}\right|

この式から、積分器は極点 $(\omega = 2k \pi，k は整数)$ のみを持ち、零点は持たず、直流信号に対して無限大の増幅を持つことがわかります。

1725542139077.png

1.2 コームフィルター#

時域では次のように表されます

yC(n)=x(n)−x(n−RM)y_C(n)=x(n)-x(n-RM)

ここで

  • R は補間因子または抽出因子
  • M は微分遅延

周波数域では次のように表されます

HC(z)=1−z−RMH_\mathrm{C}(z)=1-z^{-RM}

振幅スペクトルは次のようになります

∣HC(ejw)∣=∣1−e−jRMw∣=∣e−jRMw/2(ejRMw/2−e−jRMw/2)∣=2∣sin⁡(RM2w)∣\left|H_{\mathrm{C}}(\mathrm{e}^{\mathrm{j}w})\right|=\left|1-\mathrm{e}^{-\mathrm{j}RMw}\right|=\left|\mathrm{e}^{-\mathrm{j}RMw/2}(\mathrm{e}^{\mathrm{j}RMw/2}-\mathrm{e}^{-\mathrm{j}RMw/2})\right|=2\left|\sin\left(\frac{RM}{2}w\right)\right|

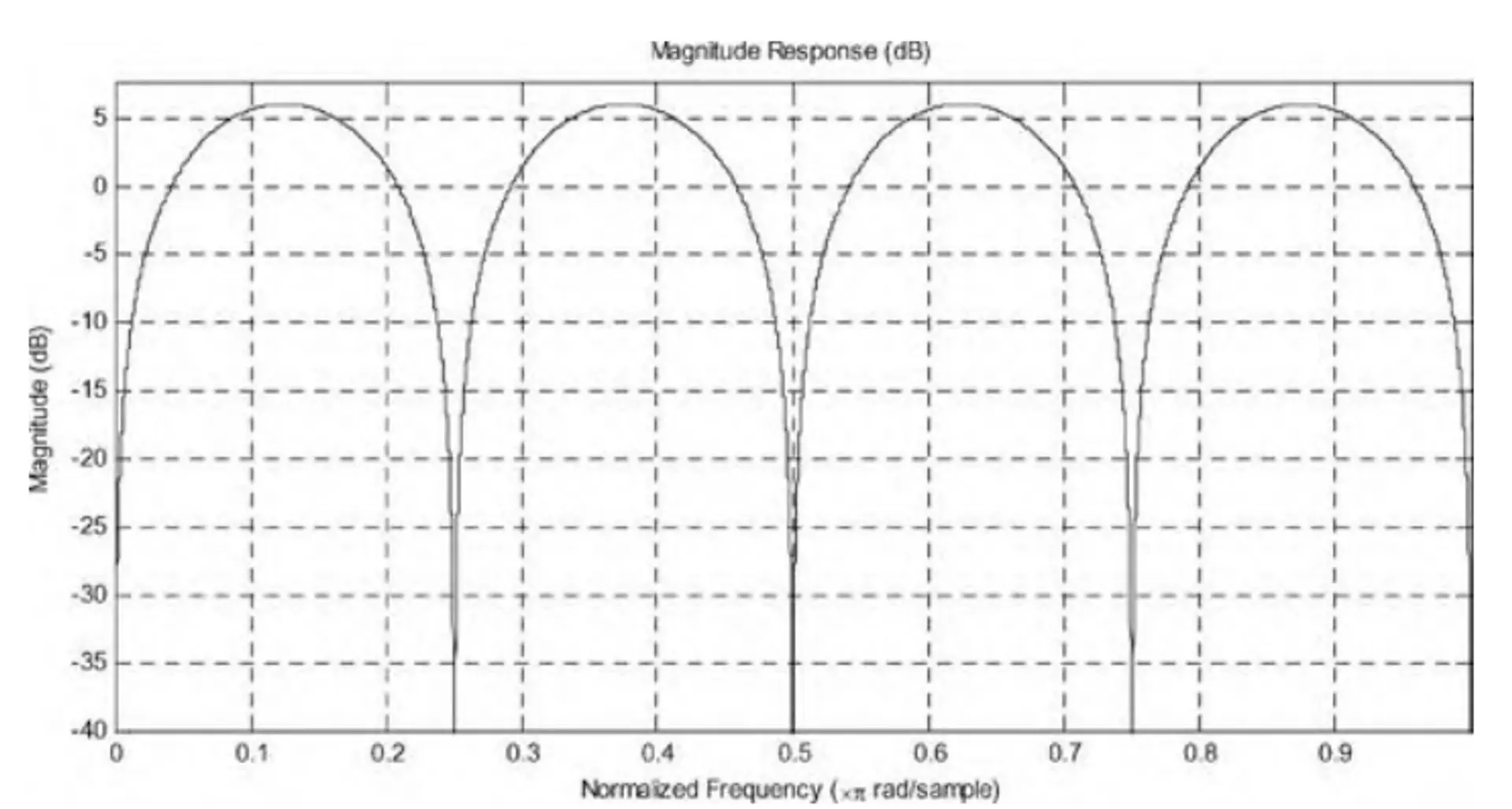
1725542829180.png

コームフィルターは零点のみを持ち、極点は持たないことがわかります。

R=8、M=1 の場合、構造は

1725542752856.png

これにより、単一級 CIC フィルターの振幅スペクトルは次のようになります

∣HCIC(ejw)∣=∣H1(ejw)∣⋅∣HC(ejw)∣=∣sin⁡(RM2w)sin⁡(w2)∣\left|H_{\mathrm{CIC}}(\mathrm{e}^{\mathrm{j}w})\right|=\left|H_{1}(\mathrm{e}^{\mathrm{j}w})\right|\cdot\left|H_{\mathrm{C}}(\mathrm{e}^{\mathrm{j}w})\right|=\left|\frac{\sin\left(\frac{RM}{2}w\right)}{\sin\left(\frac{w}{2}\right)}\right|

$\mathrm {RM\omega}/2=\mathrm {k}:\pi $ のとき、すなわち $w=\frac {2k\pi}{RM}\quad (k=\pm1,\pm2,\cdots,\pm (RM-1))$ のときに零点が決定されます。

$\omega /2 =k\pi$、すなわち $\omega = 2k\pi$ のとき、このときの振幅周波数応答は次のようになります

∣HCIC(ejω)∣ω=2kπ=RM\left|H_{\mathrm{CIC}}(\mathrm{e}^{\mathrm{j}\omega})\right|_{\omega=2k\pi}=RM

これにより、零点と極点が相殺されます。

単一級 CIC フィルターは $\omega =0$ のとき $\left| H_{CIC}(e^{j\omega}) \right|=RM$ であり、したがって主瓣の範囲は $\begin {bmatrix} 0,\frac {2\pi}{RM}\end {bmatrix}$ であり、残りはすべて副瓣であり、第一副瓣レベルは

A1=∣HCIC(ejw)∣w=3πRM=∣sin⁡(RM2×3πRM)sin⁡(12×3πRM)∣=∣1sin⁡(3π2RM)∣A_1=\left|H_{\mathrm{CIC}}(\mathrm{e}^{\mathrm{j}w})\right|_{w=\frac{3\pi}{RM}}=\left|\frac{\sin\left(\frac{RM}{2}\times\frac{3\pi}{RM}\right)}{\sin\left(\frac{1}{2}\times\frac{3\pi}{RM}\right)}\right|=\left|\frac{1}{\sin\left(\frac{3\pi}{2RM}\right)}\right|

したがって、副瓣抑制は

A=∣RMsin⁡(3π2RM)∣A=\left|RM\sin\left(\frac{3\pi}{2RM}\right)\right|

$\mathrm {R}\rightarrow\infty $ のとき、副瓣抑制は

A=20lg(lim⁡R→∞A)=20lg(3π2)=13.46dBA=20lg(\lim_{R\to\infty}A)=20lg(\frac{3\pi}{2})=13.46dB

単一級 CIC フィルターの阻止帯減衰は

α=−20lgb\alpha =-20lgb

通帯リップル（通帯波形の変動）は

δ=20lg∣bπsin⁡(bπ)∣\delta = 20lg\left|\frac{b\pi}{\sin(b\pi)}\right|

ここで b は帯域幅比率因子です。

b=Bfs/(RM)b=\frac{B}{f_s/(RM)}

単一級 CIC フィルターの副瓣レベルは高いため、多段 CIC 級聯によって改善できます。

∣H(ejw)∣=∣sin⁡(RM2w)sin⁡(w2)∣N\left|H(\mathrm{e}^{\mathrm{j}w})\right|=\left|\frac{\sin\left(\frac{RM}{2}w\right)}{\sin\left(\frac{w}{2}\right)}\right|^N

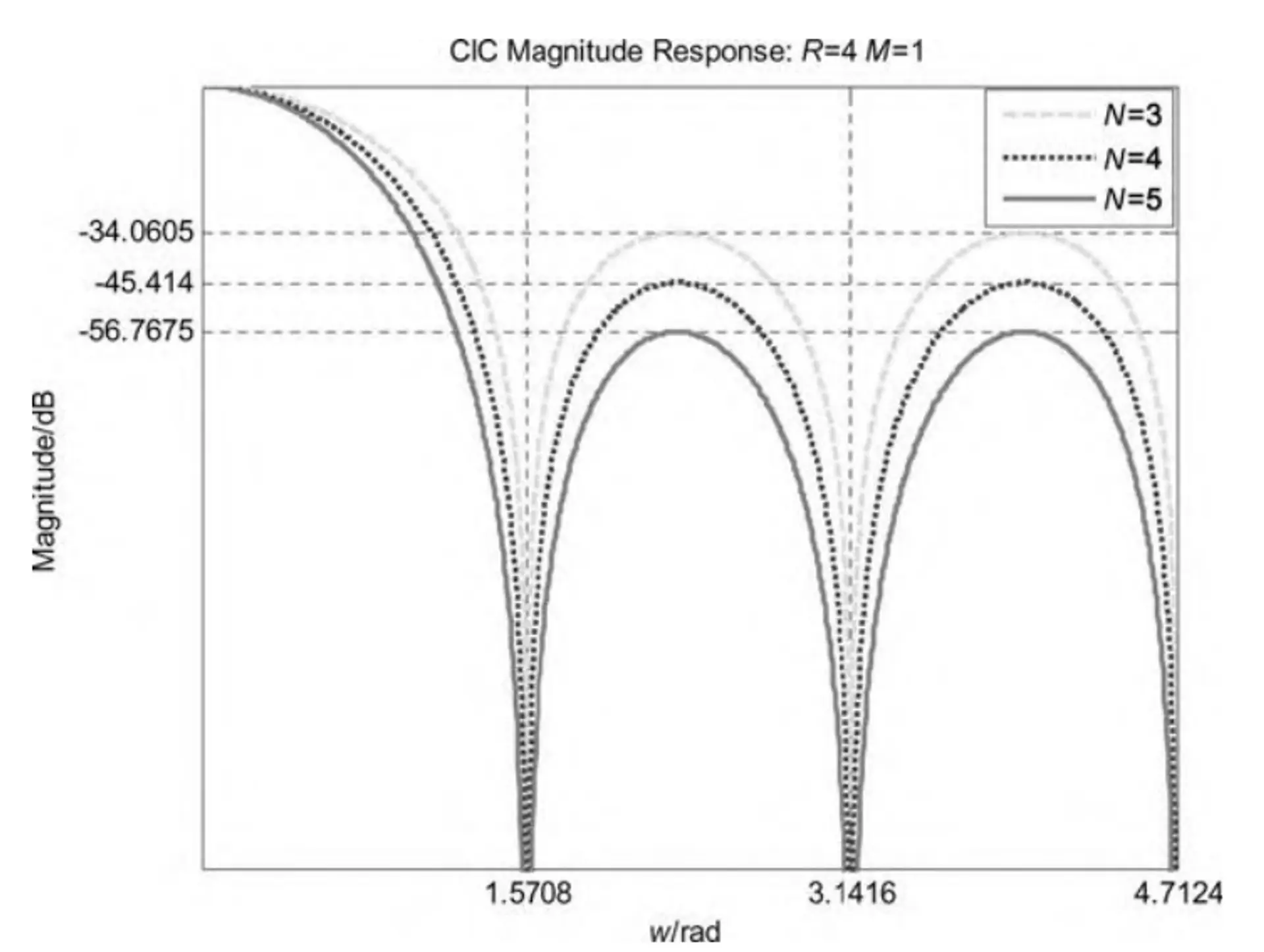
1725886131150.png

N 段 CIC 級聯フィルターに対して、副瓣抑制、阻止帯減衰、通帯リップルは次のように表されます

{AN=13.46N dBαN=−20Nlg⁡bδN=20Nlg⁡∣bπsin⁡(bπ)∣\begin{cases}A_\mathrm{N}=13.46N\:\mathrm{dB}\\\alpha_\mathrm{N}=-20N\lg b\\\delta_\mathrm{N}=20N\lg\left|\frac{b\pi}{\sin(b\pi)}\right|\end{cases}

CIC フィルターの次数を増やすと、副瓣抑制と阻止帯減衰を増加させることができますが、通帯リップルが大きくなります。したがって、通帯性能を考慮して、通常は $N\leq5$ を選択します。N が不変のとき、帯域幅比率因子 b が小さいほど、CIC フィルターの通帯と阻止帯特性も良くなるため、CIC は通常、補間システムの最後の段に配置されます（入力レートが最も高い）。

2 ビット成長問題#

多段フィルターの振幅周波数応答から、$\omega \rightarrow 0$ のとき

lim⁡w→0∣H(ejw)∣=lim⁡w→0∣RM2⋅cos⁡(RMw/2)12⋅cos⁡(w/2)∣N=(RM)N\lim\limits_{w\to0}\Bigl|H(\mathrm{e}^{\mathrm{j}w})\Bigr|=\lim\limits_{w\to0}\Biggl|\frac{\frac{RM}{2}\cdot\cos(RMw/2)}{\frac{1}{2}\cdot\cos(w/2)}\Biggr|^N=(RM)^N

これにより、多段 CIC フィルターが引き起こす可能性のある最大の振幅増益は

Gmax=(RM)NG_{max}=(RM)^N

入力データ $x (n)$ が符号付き数で、ビット幅が $B_{in}$、値の範囲が $[-2^{B_{in}-1},2^{B_{in}-1}-1]$ であると仮定すると、出力 $y (n)$ の最大値は

ymax=−2Bm−1⋅(RM)Ny_{max}=-2^{B_{\mathrm{m}}-1}\cdot\left(RM\right)^N

したがって、出力の最大ビット幅は

Bout=ceil[log⁡2∣ymax∣]+1=N⋅ceil[log⁡2(RM)]+BinB_{\mathrm{out}}=\text{ceil}[\log_2|y_{\mathrm{max}}|]+1=N\cdot\text{ceil}[\log_2(RM)]+B_{\mathrm{in}}

FPGA 設計では、出力信号のビット幅を適切に設定し、データのオーバーフローを防ぐ必要があります。リソースを節約するために、各段で適切にビットを切り捨てることもできます。

3 Matlab での CIC 補償フィルター設計#

CIC フィルターは通帯内が平坦でないため、前段に CIC 補償フィルターを追加する必要があります。Matlab の対応する関数はfdesign.ciccompで、構文は次のとおりです。

d = fdesign.ciccomp
d = fdesign.ciccomp(d,nsections,rcic)
d = fdesign.ciccomp(...,spec)
h = fdesign.ciccomp(...,spec,specvalue1,specvalue2,...)

ここで、コームフィルターの遅延長は d、フィルターの次数は nsections、CIC レート変換因子は rcic です。

3.1 例#

h = fdesign.ciccomp;
set(h,NumberOfSections=5,DifferentialDelay=1);
cicComp = design(h,'equiripple',SystemObject=true);
filterAnalyzer(cicComp)
読み込み中...
文章は、創作者によって署名され、ブロックチェーンに安全に保存されています。